GPS伪距单点定位

GPS第三次作业

这次就没什么难度了，只是照着抄公式而已，还好有聪神帮忙解读。

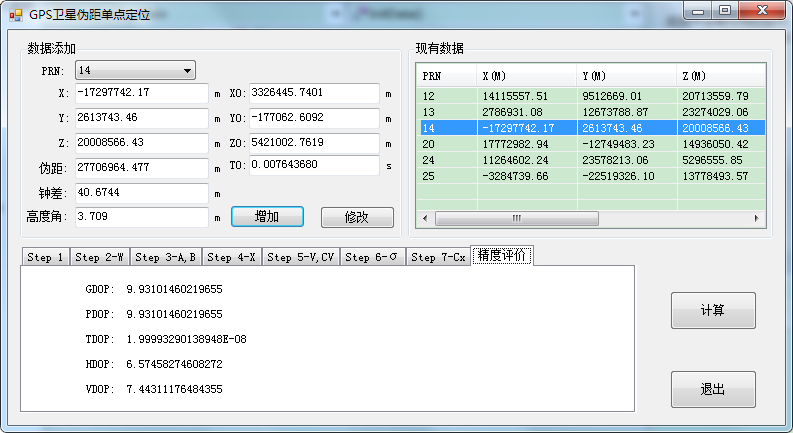
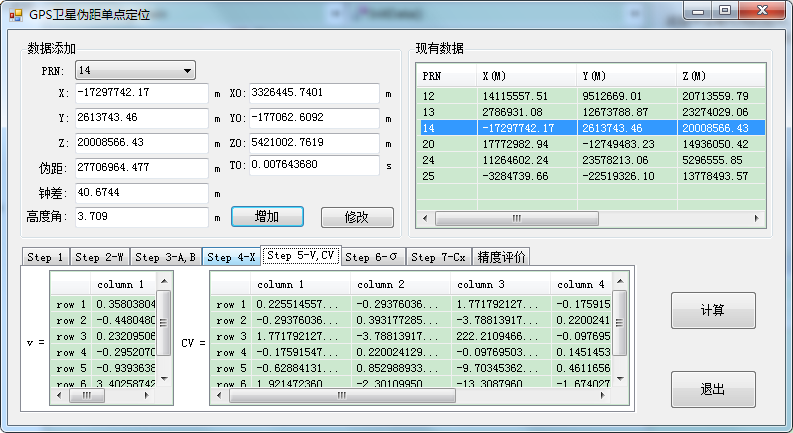
截图如下：

唯一有难度的就是矩阵的运算了，还好有人写过直接拿来用。。。

但是木有逆矩阵的计算，我又东凑西凑的找了个，还是不错的，分享下。。。

public Matrix Inverse(double[,] a, int n)    //求n阶方阵a的逆矩阵(Gauss算法)
        {
            double[,] UnitMatri=new double[n,n];//定义一个单位矩阵
            int i = 0,j;
            double temp;
            for (i = 0; i < n; i++)
            {
                UnitMatri[i, i] = 1;
            }
            for(i=0;i<n;i++)
            {
                int maxline = MaxLine(a, i, n);
                for (j = 0; j < n; j++)
                {
                    temp = a[i, j];
                    a[i, j] = a[maxline, j];
                    a[maxline, j] = temp;

                    temp = UnitMatri[i, j];
                    UnitMatri[i, j] = UnitMatri[maxline, j];
                    UnitMatri[maxline, j] = temp;
                }
                double max = a[i, i];
                for (int k = i + 1; k < n; k++)
                {
                    double r = a[k, i] / max;
                    for (int m = 0; m < n; m++)
                    {
                        a[k, m] = a[k, m] - a[i, m] * r;
                        UnitMatri[k, m] = UnitMatri[k, m] - UnitMatri[i, m] * r;
                    }
                }

            }
            for (int s = n - 1; s >= 0; s--)
            {
                double maxnew = a[s, s];
                for (i = s; i < n; i++)
                    a[s, i] = a[s, i] / maxnew;
                for (i = 0; i < n; i++)
                    UnitMatri[s, i] = UnitMatri[s,i]/ maxnew;
                for (i = s - 1; i >= 0; i--)
                {
                    maxnew = a[i, s];
                    //a[i, s] = 0;
                    for (j = 0; j < n; j++)
                    {
                        UnitMatri[i, j] = UnitMatri[i, j] - maxnew * UnitMatri[s, j];
                    }
                }
            }
            Matrix t = new Matrix(UnitMatri);
            return t;
        }