GPS第二次作业了,据小白说还是MIT的GPS作业,试了下手还是很有难度的。。。
题目:
A broadcast ephemeris file for Jan 16, 2002 is given below. All of the GPS satellites are given. For at least the set of PRN’s 4, 7, 11, 26, 27, 28 compute
(1) A 3-D plot of the trajectories of the motions of the satellites in
(a) Inertial space. Produce plots for 4 orbits of the satellites. Comment on the how closely the satellite tracks overlap.
(b) Earth fixed frame. Plots for 2 orbits of the satellites.
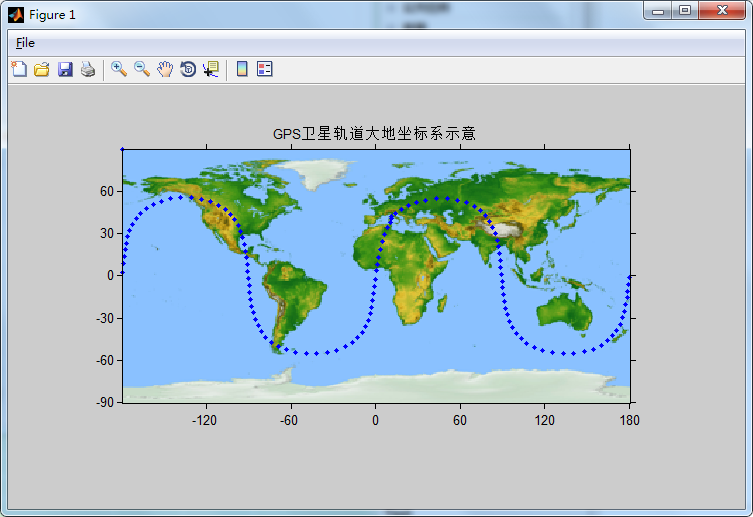
(2) A ground track plot (i.e., the track of the satellite position radially projected to the surface of the sphere). OPTIONAL: Extra credit for also showing projection on an ellipsoid (Projection of ground normal to the satellite).
(3) A sky map for geocentric location 244.5 deg Long, 35.8 deg latitude. A sky map shows azimuth and elevation as a radial plot with zenith distance scaled to a convenient distance unit.
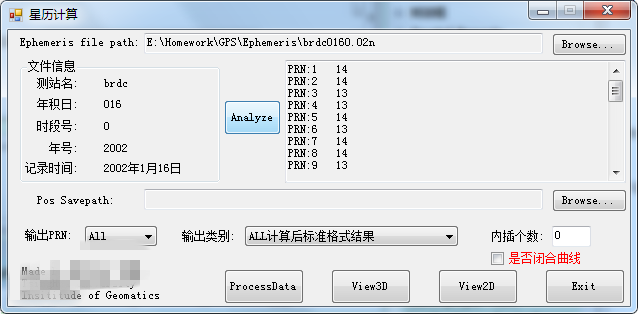
截图如下啦:
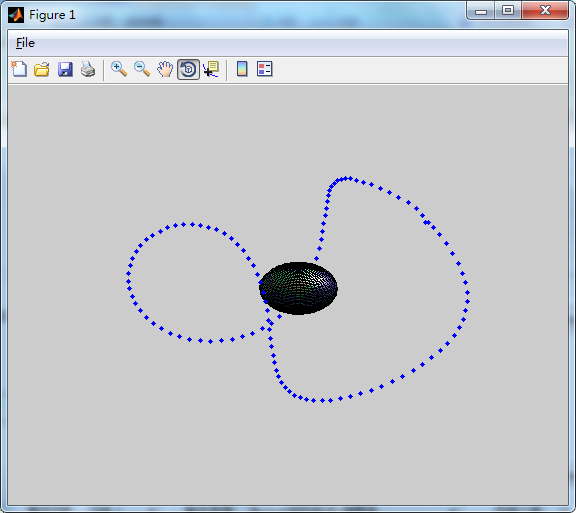
首先Matlab里画个地球
function Plot3GPS(A, titlename) cla reset; load topo; [x y z] = sphere(50); s = surface(6e6*x,6e6*y,6e6*z,'FaceColor','texturemap','CData',topo); colormap(topomap1); % Brighten the colormap for better annotation visibility: brighten(.6) % Create and arrange the camera and lighting for better visibility: %campos([1.3239 -14.4250 9.4954]); camlight; lighting gouraud; axis off vis3d;
这就搞定一个地球了,简单吧。。。
然后C#要和Matlab混编,当然用MWNumericArray进行数据的传递咯。
下面就是星历的读取,其实也很简单,按照给出的星历文档格式用Substring方法读一下就出来了。
最后就是计算XYZ和大地坐标系,大地坐标系上次作业已经搞定,这次就看看地固系里的了。
/// <summary>
/// 计算位置
/// </summary>
/// <param name="data"></param>
/// <returns></returns>
public string[] cal(GPSData data)
{
//求长半轴A
double a = data.sqa * data.sqa;
//计算平角速度
double n0 = Math.Sqrt(gm / Math.Pow(a, 3));
//计算经摄动修正后的平均角速度n
double n = n0 + data.deltan;
//计算TK
double gpstime = 0;
int gpsweek = 0;
string[] info = ReadFile.GetFileInfo(filename);
TimeChange.GetGPSTime(myear, mmonth, mday, mhour, mminute, msecond, ref gpstime, ref gpsweek);
double t = gpstime;
double tk = t - data.toe;
if (tk > 302400)
{
tk -= 604800;
}
else if (tk < -302400)
{
tk += 604800;
}
//计算MK
double mk = data.m0 + n * tk;
//计算偏近点角ek
double ek0 = mk;//初始值赋予ek
double ek = mk;
int i = 0;
do
{
ek0 = ek;
ek = mk + data.e * Math.Sin(ek0);
i++;
} while (i < 15);
//计算真近点角
vk = Math.Atan((Math.Sqrt(1 - data.e * data.e) * Math.Sin(ek)) / (Math.Cos(ek) - data.e));
//计算升交距角
double pik = vk + data.omiga;
//计算摄动改正项
double deltau = data.cuc * Math.Cos(2 * pik) + data.cus * Math.Sin(2 * pik);
double deltar = data.crc * Math.Cos(2 * pik) + data.crs * Math.Sin(2 * pik);
double deltai = data.cic * Math.Cos(2 * pik) + data.cis * Math.Sin(2 * pik);
//计算改正后的纬度参数uk
double uk = pik + deltau;
//计算改正后的向径rk
double rk = a * (1 - data.e * Math.Cos(ek)) + deltar;
//计算改正后的倾角
double ik = data.i0 + deltai + data.i1 * tk;
//计算卫星在轨道平面内的坐标xk1,yk1
double xk1 = rk * Math.Cos(uk);
double yk1 = rk * Math.Sin(uk);
//计算改正升交点的经度
double omigak = data.omiga0 + (data.omiga1 - omigae) * tk - omigae * data.toe;
//计算卫星在地固系中的坐标
double xk = xk1 * Math.Cos(omigak) - yk1 * Math.Cos(ik) * Math.Sin(omigak);
double yk = xk1 * Math.Sin(omigak) + yk1 * Math.Cos(ik) * Math.Cos(omigak);
double zk = yk1 * Math.Sin(ik);
//计算轨道面坐标系
double x1 = xk1;
double y1 = yk1 * Math.Cos(ik);
。。。
return 。。。;
}
这些也都是基本的公式,照着书本copy下就好了,最后就能得出上面的图啦。
哦,还有插值采用的是最简单得拉格朗日了,应该是均匀差值。
写了快一周了,疯了。。。